递归的概念
简单的说:递归就是方法调用自己,每次调用传入不同的变量。递归有助于编程者解决复杂的问题,同时可以让代码变得简洁
两个案列说明递归的调用机制
1
2
3
4
5
6
7
8
9
10
11
12
| public class Demo1 {
public static void main(String[] args) {
test(4);
}
public static void test(int n){
if(n>2){
test(n-1);
}
System.out.println("n="+n);
}
}
|
建议先自己分析一下这个运行结果是啥!
然后在idea里面编译运行看一下结果,是不是和你想的一样。
递归调用的规则:
1.当程序执行到一个方法时,就会开辟一个独立的空间(栈 )
2.就像上面的案例,当执行test(4)时,因为n>2,所以开始执行test(3),注意此时test(4)是未执行完的,直到test(2),test(3)完毕出栈之后,最后才是test(4)
3.每个空间的数据(局部变量,是独立的)
再来一个例子
1
2
3
4
5
6
7
8
9
10
11
12
|
class Demo2{
puclic static void main(String[] args){
System.out.println(fun(4));
}
public static int fun(int n){
if(n==1){
return 1;
}
return n*fun(n-1);
}
}
|
递归需要遵守的重要规则
1)执行一个方法时,就创建一个新的受保护的独立空间(栈空间)
2)方法的局部变量时独立的,不会相互影响
3)如果方法中应用的是引用类型的变量(比如数组),就会共享该引用类型的数据
3)递归必须向退出递归的条件逼近,否则就是无限递归,死龟!
4)当一个方法执行完毕,或者遇到return,就会返回,遵守谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕。
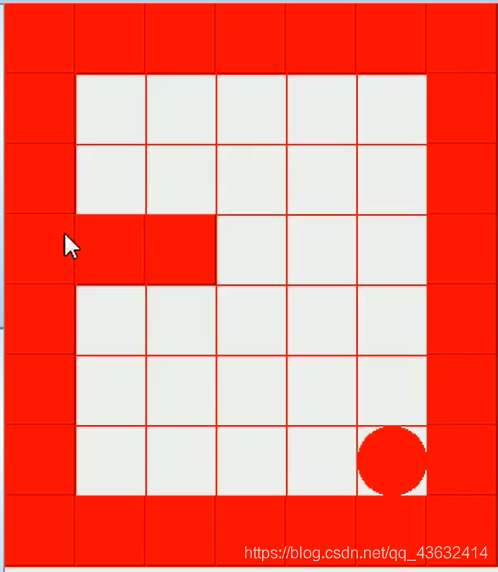
经典迷宫问题
问题:小球从坐标位置为(1,1)的空白位置移动到(6,5)的最短路径怎么用回溯的思想求出来(注:左上角的坐标是(0,0))
提示:
- 小球得到的路径,和程序员设置的找路策略有关即:找路的上下左右的顺序相关
- 在得到小球路径时,可以先使用(下右上左),再改成(上右下左),看看路径是不是有变化
- 测试回潮现象
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
|
public class MiGong {
public static void main(String[] args) {
int[][] map = new int[8][7];
for (int i = 0; i < 7; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
map[1][2] = 1;
map[2][2] = 1;
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
setWay(map, 1, 1);
System.out.println("输出新的地图,小球走过,并标识过的递归");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
public static boolean setWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {
return true;
} else {
if (map[i][j] == 0) {
map[i][j] = 2;
if (setWay(map, i + 1, j)) {
return true;
} else if (setWay(map, i, j + 1)) {
return true;
} else if (setWay(map, i - 1, j)) {
return true;
} else if (setWay(map, i, j - 1)) {
return true;
} else {
map[i][j] = 3;
return false;
}
} else {
return false;
}
}
}
}
|